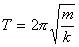Movimiento Armonico Simple 

El estudio del oscilador armónico constituye en Física un capítulo muy importante, ya que son muchos los sistemas físicos oscilantes que se dan en la naturaleza y también muchos han sido producidos por el hombre.

 

 

 

 

 

 

 

 

 

 

DEFINICION

Una partícula describe un Movimiento Armónico Simple (M.A.S.) cuando se mueve a lo largo del eje X, estando su posición x dada en función del tiempo t por la ecuación

 

 

 

 

 

 

 

CARACTERISTICAS DE UN M.A.S:

-Como los valores máximo y mínimo de la función seno son +1 y -1, el movimiento se realiza en una región del eje X comprendida entre +A y     -A. 

 

-La función seno es periódica y se repite cada 2p, por tanto, el movimiento se repite cuando el argumento de la función seno se incrementa en 2p, es decir, cuando transcurre un tiempo T tal que

 

 

 

 

 

 

CINEMATICA DE UN M.A.S:

En un movimiento rectilíneo, dada la posición de un móvil, obtenemos la velocidad derivando respecto del tiempo y luego, la aceleración derivando la expresión de la velocidad.

 

 

 

ELEMENTOS:

1. Oscilación o vibración: es el movimiento realizado desde cualquier posición hasta regresar de nuevo a ella pasando por las posiciones intermedias.

2. Elongación: es el desplazamiento de la partícula que oscila desde la posición de equilibrio hasta cualquier posición en un instante dado.

3. Amplitud: es la máxima elongación, es decir, el desplazamiento máximo a partir de la posición de equilibrio.

4. Periodo: es el tiempo requerido para realizar una oscilación o vibración completa. Se designa con la letra "t".

5. Frecuencia: es el número de oscilación o vibración realizadas en la unidad de tiempo.

6. Posición de equilibrio: es la posición en la cual no actúa ninguna fuerza neta sobre la partícula oscilante.

 

 

 

DINAMICA DE UN M.A.S:

Aplicando la segunda ley de Newton obtenemos la expresión de la fuerza necesaria para que un móvil de masa m describa un M.A.S. Esta fuerza es proporcional al desplazamiento x y de sentido contrario a éste.

 

 

 

 

En la ecuación anterior vemos que la fuerza que origina un movimiento armónico simple es una fuerza del tipo:

 

 

es decir una fuerza como la que hace un muelle, directamente proporcional a la elongación pero de signo contrario. K es la constante recuperadora o constante de elasticidad y se puede observar, en las dos ecuaciones anteriores, que está relacionada con la pulsación:

 

 

 

 

Teniendo en cuenta que w = 2p / T podemos deducir el periodo del movimiento armónico simple: