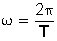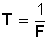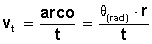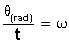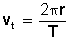Movimiento Armonico Simple 

La descripción de un movimiento circular puede hacerse bien en función de magnitudes lineales ignorando la forma de la trayectoria (y tendremos velocidad y aceleración tangenciales), o bien en función de magnitudes angulares (y tendremos velocidad y aceleración angulares). 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

EL RADIAN

Si tenemos un ángulo cualquiera y queremos saber cuánto mide, tomamos un transportador y lo medimos. Esto nos da el ángulo medido en grados. Este método viene de dividir la circunferencia en 360º, y se denomina sexagesimal.

 

Para medir un ángulo en radianes se mide el largo del arco (s) abarcado por el ángulo θ de la figura a la izquierda. Esto se puede hacer con un centímetro, con un hilito o con lo que sea. También se mide el radio del círculo.

Para obtener el valor del ángulo (θ) en radianes usamos la fórmula:

 

 

 

 

Hacer la división del arco sobre radio significa ver cuántas veces entra el radio en el arco. Como el radio y el arco deben medirse en la misma unidad, el radián resulta ser un número sin unidades.Esto significa que el valor del ángulo en radianes solo me indica cuántas veces entra el radio en el arco. Por ejemplo, si el ángulo θ mide 3 radianes, eso significa que el radio entra 3 veces en el arco abarcado por ese ángulo

Si quisiéramos calcular o conocer al valor del arco, hacemos:

 

 

 

 

PERIODO Y FRECUENCIA

El periodo (T) de un movimiento circular es el tiempo que tarda una partícula o un cuerpo en realizar una vuelta completa, revolución o ciclo completo.

 

 

 

 

La frecuencia (F) de un movimiento circular al número de revoluciones, vueltas o ciclos completos durante la unidad de tiempo. La unidad utilizada para cuantificar (medir) la frecuencia de un movimiento es el hertz (Hz), que indica el número de revoluciones o ciclos por cada segundo.

 

 

 

 

 

POSICIÓN ANGULAR (θ)

Podemos imaginar, como ejemplo, que se tiene una piedra amarrada a una cuerda y la movemos en círculos de radio r. En un instante de tiempo t el móvil (en nuestro caso la piedra) se encuentra en el punto P. Su posición angular (lo que la piedra ha recorrido en la circunferencia) viene dada por el ángulo θ, formado por el punto P, el centro de la circunferencia C y el origen O (desde donde empezó a girar la piedra).

 

 

 

VELOCIDAD ANGULAR(ω)

De manera sencilla: en el movimiento circular la velocidad angular está dada por la cantidad de vueltas que un cuerpo da por segundo.

 

Otra manera de decir lo mismo sería: en el movimiento circular la velocidad angular está dada por el ángulo recorrido (θ) dividido por unidad de tiempo. El resultado está en grados por segundo o en rad por segundo.

 

 

 

ω = velocidad angular en rad/seg.

θ = desplazamiento angular en rad.

t = tiempo en segundos en que se efectuó el desplazamiento angular.

 

La velocidad angular también se puede determinar si sabemos el tiempo que tarda en dar una vuelta completa o periodo (T):

 

 

 

 

 

 

 

 

Como                                   Entonces

 

 

 

Aquí debemos apuntar que una misma velocidad angular se puede expresar de varias maneras diferentes.

Por ejemplo, pasar una velocidad de 60 rpm a varias unidades diferentes:

 

 

 

 

 

 

VELOCIDAD TANGENCIAL(v)

Para calcular la velocidad tangencial hacemos: espacio recorrido sobre la circunferencia (o arco recorrido) dividido por el tiempo empleado, que expresamos con la fórmula:

 

                                                 

                                                    Pero como                                              Entonces

 

 

 

Como la velocidad angular (ω) también se puede calcular en función del periodo

 

 

(T) con la fórmula                                     

 

 

y la velocidad tangencial siempre está en función del radio, entonces la fórmula

 

 

Se convierte en